What is Chi-Squared analysis ?
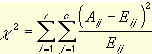
Good Question. (By the way it's pronounced KYE squared). If you search for Chi-squared in a search engine you're likely to get an extract from a university thesis with a mass of uninspiring Greek symbols and gobbledegook . Many people wouldn't understand them. Well I hope so because I can't understand them either.
There are some good examples on the internet (but not about lotteries), many of them about the characteristics of fruit flies, or the incidence of various diseases in certain groups of society. However the best and simplest introduction takes one through a few exercises and leads on to chi-square. It's a lesson by Amar Patel :- Chi-square-introduction.
A more technical discussion can be found at:-
the Southwest Missouri State university Web site :- David.W.Stockburger.
However if you don't have an hour or so to spare, chi-square is just a test to see if your theory is backed by your experimental results.
Put simply, there has to be a test which enables you to look at some experimental or survey results and decide whether the results are telling you something significant, or whether normal random variations account for what you thought were meaningful figures leading you to a conclusion.
Normal Chi square analysis returns a value which can be any number , but reference to a chi square distribution graph is required in order to make a decision from this value.
I'm not a statistician but I'm pretty good at Microsoft Excel. This spreadsheet has an in built function called CHITEST which does it all in one go. This test returns a value between 0 and 1 which is a measure of how accurately theoretical values match those obtained by experiment. You can use it to test a hypothesis, and the closer the result is to 1 the more reality approaches your hypothesis. Conversely, if your hypothesis isn't sound, then chi-squared values will fall , and if consistently zero, then your hypothesis was incorrect.
Chi squared and the lottery
To use Chi-squared on the lottery you first have to have a hypothesis to test actual results against. If you assume that the lottery machines are fair and impartial, using identical sets of fair balls, you might reasonably expect that in time, as the number of balls drawn increases that all balls will be drawn (totalling from draw no.1 ) by the same approximate number of times.
You might assume also that this theoretical number of times was equal to the total number of balls drawn divided by 49. This would mean that by draw number 70 each ball should have been drawn (70 x 7 )/49 times = 10 times. You could calculate this figure for each draw number, and use it as your expected figure for all 49 balls, and then using the actual draw results on corresponding weeks, update the ball count for each ball and work out the chi-squared figure on a week by week basis over lottery history.
You'd need to be able to use a spreadsheet such as Excel with CHITEST combined with visual basic code to do the maths and plot the graphs.
The "error" in this case would be (for each draw ) the difference between the actual number of times each ball has been drawn, and the hypothesis value, of (draw number /7) which gradually increases with the draw number.
For any Lottery based on 49 balls, drawing 7 balls per draw , this process always gives a chi squared value for draw 1 of 0.7160 .This is because there is initially no history (or ball count ) to compare the hypothesis with (all ball totals are zero before draw 1 ) , so the chi-squared calculation just happens to return 0.7160. From draw 2 onwards for a few draws Chi-square invariably rises, because there is more chance of a ball never drawn before coming out in the early weeks and this agrees with the hypothesis that ball counts will equal out eventually. Note the higher (closer to 1 Chi square gets, the more your theory is substantiated. )
If this exercise resulted in consistent , near 1.000 values week after week then this would mean a good strategy might be to back the "cold" infrequently chosen balls. However there'd be no guarantee they'd all come out the same week though ! I have tested the UK lottery results against this hypothesis and the results are shown on:-
To assess how differing results might have changed the chi square results and assess how volatile chi-squared is to discrepancies between reality and the hypothesis ,I carried out simulations using random numbers as "fantasy lotteries". This revealed how different trends in selection can create a different looking graph.
So is It worth doing chi-squared analysis ? the jury is still out, but the graphs are fun.